刘昭宏 (Zhaohong Liu)

Robotics researcher, M.Sc. Mech (SJTU), B.E. Aircraft Control (NWPU).

3 minute read

1. Overall Architecture

The Transformer is a sequence-to-sequence neural architecture based entirely on self-attention mechanisms, without recurrence or convolution. It consists of two main parts:

  • Encoder: Generates contextualized representations of input sequences.
  • Decoder: Autoregressively generates output sequences based on encoder output and previously generated tokens.

Transformer Architecture

Figure: Transformer Architecture

Step 1: Input Embedding

Input takes word embedding and position embedding, and adds them together. The result is passed to the encoder.

\[\text{Input} = \text{Embedding}(x) + \text{PositionEmbedding}(x)\]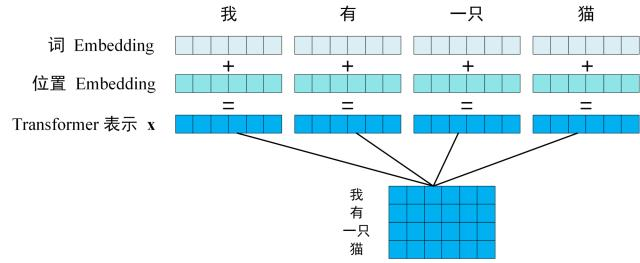

Transformer Input Embedding

Figure: Transformer Input Embedding

Step 2: Encoder

Input vector is represented as a matrix $X \in \mathbb{R}^{n \times d_{\text{model}}}$, where $n$ is the sequence length and $d_{\text{model}}$ is the embedding dimension. The encoder consists of $N$ identical layers, each with two sub-layers:

  1. Multi-head self-attention (MHA)
  2. Feed-forward network (FFN)

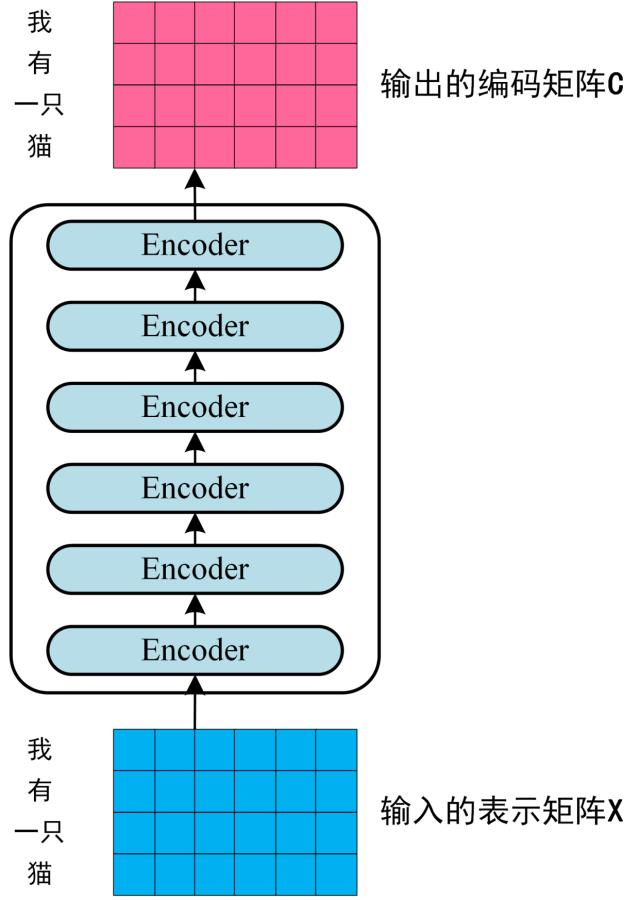
Encoder

Figure: Encoder Process

Step 3: Decoder

The decoder also consists of $N$ identical layers, each with three sub-layers:

  1. Masked multi-head self-attention (MHA)
  2. Multi-head self-attention (MHA) with encoder output as keys and values
  3. Feed-forward network (FFN)

The use of Masked MHA ensures that the prediction for a given position depends only on the known outputs at previous positions.

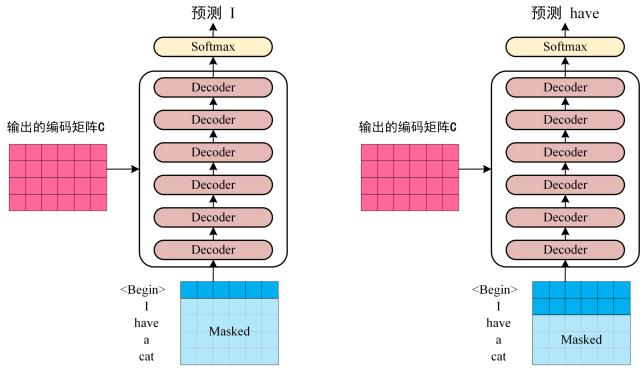
Decoder Prediction

Figure: Decoder Prediction

Step 4: Output

The decoder output is passed through a linear layer followed by a softmax function to produce the final output probabilities for the next token in the sequence.

\[\text{Output} = \text{softmax}(\text{DecoderOutput} \times W_{\text{embedding}}^T)\]

Where $W_{\text{embedding}}$ is the learned embedding matrix. The softmax function converts the logits into probabilities for each token in the vocabulary.

2. Input of Transformer

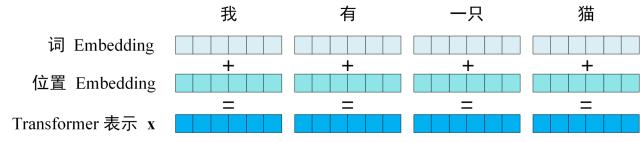
Transformer Input

Figure: Transformer Input

2.1 Word Embedding

  • Input tokens are mapped to embedding vectors using learned embeddings.
  • Embedding dimension: $d_{\text{model}}$ (typically 512).

2.2 Positional Embedding

  • Added to embeddings to inject positional information.
  • Fixed sinusoidal positional embeddings used:
\[PE_{(pos,2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)\] \[PE_{(pos,2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)\]

3. Self-Attention

MHA
(left) Scaled Dot-Product Attention. (right) Multi-Head Attention consists of several attention layers running in parallel.

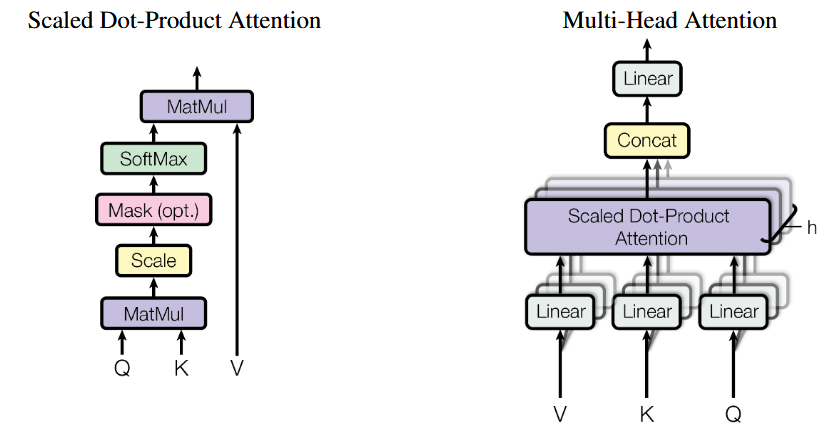
3.1 Architecture of Self-Attention

In practice, we compute the attention function on a set of queries simultaneously, packed together into a matrix $Q$. The keys and values are also packed together into matrices $K$ and $V$.

Self-attention maps queries (Q), keys (K), and values (V) to an output via scaled dot-product attention:

\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]
  • $Q, K, V$: matrices of queries, keys, and values.
  • $d_k$: dimension of queries and keys.

3.2 Calculating Q, K, V

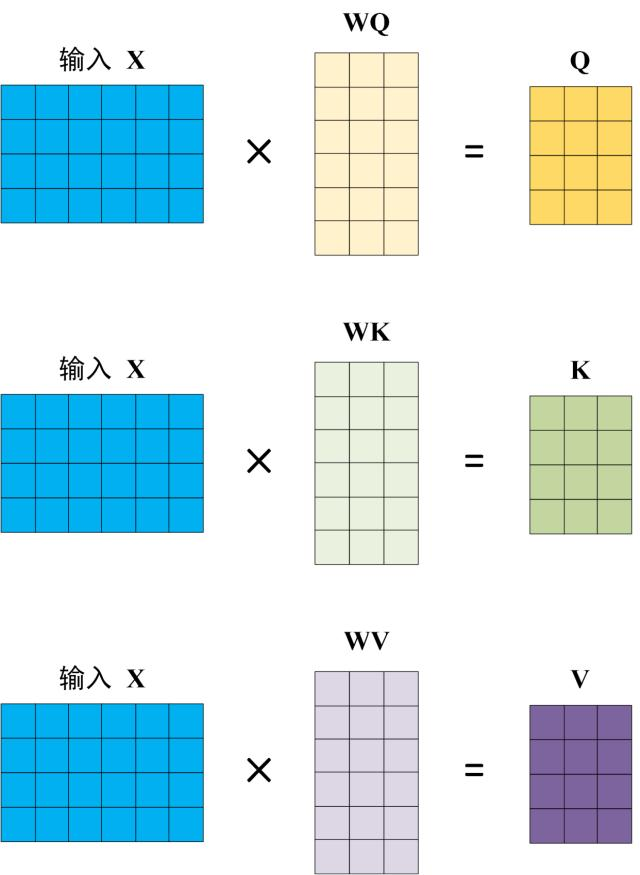
Calculating Q, K, V

Figure: Calculating Q, K, V

Computed via learned linear projections from input embeddings ($X$):

\[Q = X W^Q,\quad K = X W^K,\quad V = X W^V\]

Where $W^Q, W^K, W^V$ are learned parameter matrices.

First calculate the $Q K^T$:

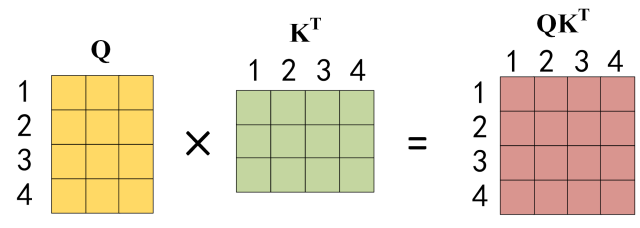
Calculating QK^T

Figure: Calculating $Q K^T$

Then apply the softmax function to each row to get the attention weights:

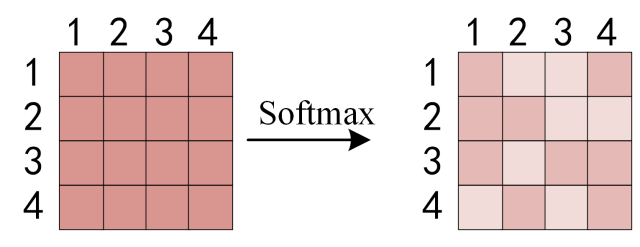
softmax

Figure: Apply softmax on rows

Multiply the attention weights with the values to get the output:

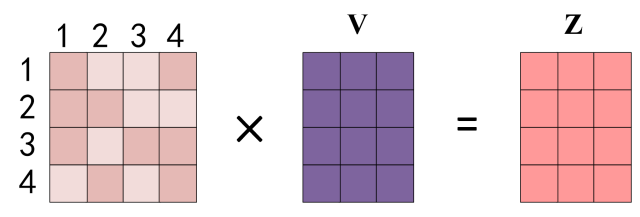
softmax

Figure: Multiply values

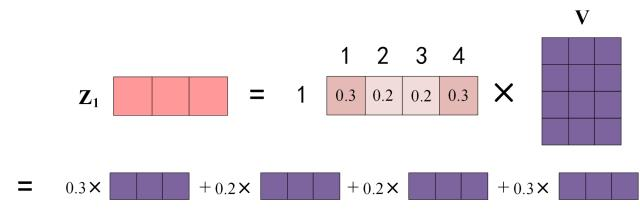
softmax

Figure: Get Output Z

3.3 Output of Self-Attention

  • Weighted sum of values based on attention scores.
  • Output dimension matches input embedding size ($d_{\text{model}}$).

3.4 Multi-Head Attention (MHA)

Multiple parallel attention heads run independently, then concatenate:

\[\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O\]

Each head computes:

\[\text{head}_i = \text{Attention}(Q W_i^Q, K W_i^K, V W_i^V)\]
  • Typically, $h=8$, each head dimension $d_k = d_v = d_{\text{model}}/h$.

4. Architecture of Encoder

Transformer Arch
The Transformer - model architecture.

4.1 Add and LayerNorm

Each encoder layer includes residual connections and layer normalization:

\[x = \text{LayerNorm}(x + \text{Sublayer}(x))\]
  • Applied after Multi-head Self-Attention and Feed-Forward layers.

4.2 Feed Forward

Position-wise fully-connected feed-forward network (FFN):

\[\text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2\]
  • Intermediate dimension typically $d_{ff}=2048$.

4.3 Input and Output Calculation of Encoder

Overall encoder-layer calculation per layer:

\[x = \text{LayerNorm}(x + \text{MultiHeadSelfAttn}(x))\] \[x = \text{LayerNorm}(x + \text{FFN}(x))\]
  • Encoder stack repeats this structure $N=6$ times.

5. Architecture of Decoder

Decoder consists of 6 identical layers, each with three sub-layers.

5.1 First MHA in Decoder Block

  • Masked self-attention prevents tokens from attending to future positions.
  • Computation is similar to encoder self-attention, but with a causal mask:
\[x = \text{LayerNorm}(x + \text{MaskedMultiHeadSelfAttn}(x))\]

5.2 Second MHA in Decoder Block (Encoder-Decoder Attention)

  • Queries come from previous decoder sub-layer.
  • Keys and values come from the final encoder output:
\[x = \text{LayerNorm}(x + \text{MultiHeadAttn}(x, \text{EncoderOutput}, \text{EncoderOutput}))\]

5.3 Softmax Prediction

  • After decoder stack, the final decoder representation is projected to vocabulary logits:
\[\text{logits} = \text{DecoderOutput} \times W_{\text{embedding}}^T\]
  • Softmax function predicts next token probabilities:
\[P(y_i \mid y_{<i}, x) = \text{softmax}(\text{logits})\]

References

Transformer Architecture provides a powerful parallelizable structure for sequence modeling, relying entirely on attention mechanisms to encode global dependencies efficiently.

You may also enjoy